分位数概念深度探
分位数概念深度探
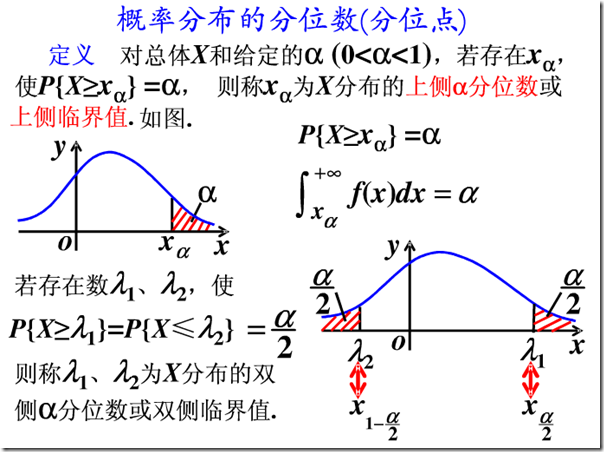
在统计学中,分位数是一个非常重要的概念,它常常被用来描述数据集的分布情况。在日常的统计分析中,我们经常遇到各种各样的分位数,比如百分位数、四分位数等。本文将为大家详细探讨分位数的概念和用途。
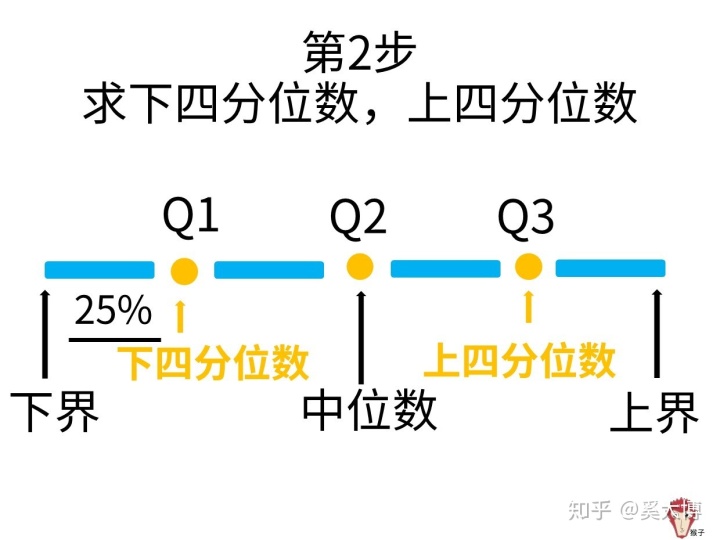
一、什么是分位数?

简单来说,分位数是将一个数据集按照从小到大的顺序进行排列后,位于某个特定位置的数值。例如,在一组数据中,中位数就是位于中间位置的数值,而四分位数则是将数据分为四个等份的数值。
二、分位数的计算方法
分位数的计算方法因不同的分位数而异。对于百分位数,我们通常需要先对数据进行排序,然后根据所需的百分位数值确定数据在排序后的位置。例如,第50百分位数就是将数据排序后位于中间的那个数,第25百分位数则是位于前四分之一的数据。对于其他类型的分位数,其计算方法也有所不同。
三、分位数的应用场景
分位数在统计分析和数据处理中有着广泛的应用。例如,在描述一组数据的分布情况时,我们可以使用中位数、四分位数等来描述数据的集中趋势和离散程度。此外,在质量检测、产品质量评估等方面,分位数也被广泛应用。例如,我们可以通过检测产品的不良率或合格率来计算某个特定百分位数的数值,从而了解产品质量的好坏情况。
四、常见误解和误区
在处理数据时,有些人可能会对分位数的概念产生误解。例如,有些人可能会认为百分位数越大的数值就一定越大,或者认为中位数就是平均数。实际上,这些概念是不同的。分位数是根据数据集的排列顺序来确定的特定位置的数值,而平均数则是所有数值的总和除以数值的个数。因此,在处理数据时,我们需要正确理解分位数的概念和计算方法。
五、总结
分位数是统计学中一个非常重要的概念,它可以帮助我们更好地了解数据集的分布情况。无论是百分位数还是四分位数等不同类型的分位数,其计算方法和应用场景都有所不同。因此,在处理数据时,我们需要正确理解分位数的概念和计算方法,并根据实际需求选择合适的分位数来描述数据集的分布情况。同时,我们也要注意避免常见的误解和误区,以免影响数据的分析和处理结果。


























