std 标准差含义
std 标准差含义
在日常数据分析过程中,标准差(Standard Deviation)是统计计算中的一个常见指标。我们常会见到这一概念在各种统计报告、科研论文、数据分析报告中。那么,标准差具体指的是什么呢?

什么是标准差?
标准差是用于描述一组数值的离散程度的一种量度。它反映的是这些数值与其平均值之间的差异程度。简而言之,标准差越大,意味着这组数据的波动范围越广,数值的分布就越不集中;反之则越小。
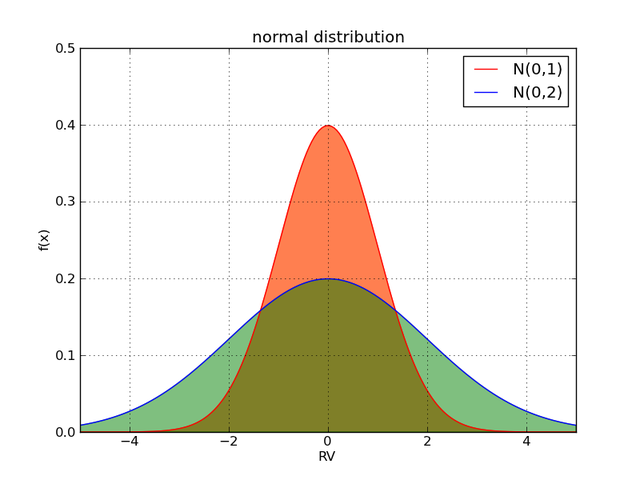
标准的计算方式
计算标准差的公式主要涉及到数据的方差。方差表示每个数值与均值之差的平方的平均数,再乘以该组数的数量取平均的倒数的平方根就是标准差的数值了。虽然手算复杂且易出错,但是现在的很多数据分析工具可以非常快速且准确地进行这个计算。
标准差在现实生活中的应用
-
评估风险: 在投资理财或预测消费时,可以通过观察某类数据或项目的标准差,评估其波动或变化可能带来的风险大小。一般而言,风险较高的产品往往伴随着较大的标准差。
-
比较数据的分布: 在处理一些大规模的样本数据时,比如各种商品的价格分布,通过观察其标准差的大小,我们可以更好地理解价格的集中趋势和分散程度。
-
统计检测: 在科学实验或医学研究中,标准差也常被用来检测样本数据是否符合某种预期的分布模式或是否具有显著性差异。
总结
总的来说,标准差是一个非常重要的统计指标,它为研究者提供了一个清晰的方式去衡量和评估一组数值的变化和分布状况。掌握标准差的相关知识和使用技巧可以帮助我们更好地分析、解释数据并从中提取出有价值的信息。
由于篇幅原因,这次就为大家讲解了这么多关于std标准差的内容。如果需要更深入地了解或者涉及其他统计指标,欢迎继续提问和探讨。


























